Triangles | Exercise 7.3 | NCERT Solution Maths 9 | Chapter 7

Exercise: 7.3 (Page No: 128)

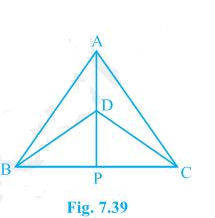
1. ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that

(i) ΔABD ≅ ΔACD

(ii) ΔABP ≅ ΔACP

(iii) AP bisects ∠A as well as ∠D

(iv) AP is the perpendicular bisector of BC.

Solution:

In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.

(i) ΔABD and ΔACD are similar by SSS congruency because:

AD = AD (It is the common arm)

AB = AC (Since ΔABC is isosceles)

BD = CD (Since ΔDBC is isosceles)

∴ ΔABD ≅ ΔACD.

(ii) ΔABP and ΔACP are similar as:

AP = AP (It is the common side)

∠PAB = ∠PAC (by CPCT since ΔABD ≅ ΔACD)

AB = AC (Since ΔABC is isosceles)

So, ΔABP ≅ ΔACP by SAS congruency condition.

(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.

AP bisects ∠A. — (i)

Also, ΔBPD and ΔCPD are similar by SSS congruency as

PD = PD (It is the common side)

BD = CD (Since ΔDBC is isosceles.)

BP = CP (by CPCT as ΔABP ≅ ΔACP)

So, ΔBPD ≅ ΔCPD.

Thus, ∠BDP = ∠CDP by CPCT. — (ii)

Now by comparing (i) and (ii) it can be said that AP bisects ∠A as well as ∠D.

(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ΔCPD)

and BP = CP — (i)

also,

∠BPD +∠CPD = 180° (Since BC is a straight line.)

⇒ 2∠BPD = 180°

⇒ ∠BPD = 90° —(ii)

Now, from equations (i) and (ii), it can be said that

AP is the perpendicular bisector of BC.

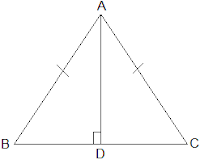
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that

(i) AD bisects BC (ii) AD bisects ∠A.

Solution:

It is given that AD is an altitude and AB = AC. The diagram is as follows:

(i) In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°

AB = AC (It is given in the question)

AD = AD (Common arm)

∴ ΔABD ≅ ΔACD by RHS congruence condition.

Now, by the rule of CPCT,

BD = CD.

So, AD bisects BC

(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD

Hence, AD bisects ∠A.

3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see Fig. 7.40). Show that:

(i) ΔABM ≅ ΔPQN

(ii) ΔABC ≅ ΔPQR

Solution:

Given parameters are:

AB = PQ,

BC = QR and

AM = PN

(i) ½ BC = BM and ½ QR = QN (Since AM and PN are medians)

Also, BC = QR

So, ½ BC = ½ QR

⇒ BM = QN

In ΔABM and ΔPQN,

AM = PN and AB = PQ (As given in the question)

BM = QN (Already proved)

∴ ΔABM ≅ ΔPQN by SSS congruency.

(ii) In ΔABC and ΔPQR,

AB = PQ and BC = QR (As given in the question)

∠ABC = ∠PQR (by CPCT)

So, ΔABC ≅ ΔPQR by SAS congruency

4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Solution:

It is known that BE and CF are two equal altitudes.

Now, in ΔBEC and ΔCFB,

∠BEC = ∠CFB = 90° (Same Altitudes)

BC = CB (Common side)

BE = CF (Common side)

So, ΔBEC ≅ ΔCFB by RHS congruence criterion.

Also, ∠C = ∠B (by CPCT)

Therefore, AB = AC as sides opposite to the equal angles is always equal.

5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.

Solution:

In the question, it is given that AB = AC

Now, ΔABP and ΔACP are similar by RHS congruency as

∠APB = ∠APC = 90° (AP is altitude)

AB = AC (Given in the question)

AP = AP (Common side)

So, ΔABP ≅ ΔACP.

∴ ∠B = ∠C (by CPCT)