Access Answers of NCERT Class 9 Maths Chapter 2 – Polynomials
Exercise 2.1 Page: 32
1. Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x2–3x+7
Solution:
The equation 4x2–3x+7 can be written as 4x2–3x1+7x0
Since x is the only variable in the given equation and the powers of x (i.e., 2, 1 and 0) are whole numbers, we can say that the expression 4x2–3x+7 is a polynomial in one variable.
(ii) y2+√2
Solution:
The equation y2+√2 can be written as y2+√2y0
Since y is the only variable in the given equation and the powers of y (i.e., 2 and 0) are whole numbers, we can say that the expression y2+√2 is a polynomial in one variable.
(iii) 3√t+t√2
Solution:
The equation 3√t+t√2 can be written as 3t1/2+√2t
Though, t is the only variable in the given equation, the powers of t (i.e.,1/2) is not a whole number. Hence, we can say that the expression 3√t+t√2 is not a polynomial in one variable.
(iv) y+2/y
Solution:
The equation y+2/y an be written as y+2y-1
Though, y is the only variable in the given equation, the powers of y (i.e.,-1) is not a whole number. Hence, we can say that the expression y+2/y is not a polynomial in one variable.
(v) x10+y3+t50
Solution:
Here, in the equation x10+y3+t50
Though, the powers, 10, 3, 50, are whole numbers, there are 3 variables used in the expression
x10+y3+t50. Hence, it is not a polynomial in one variable.
2. Write the coefficients of x2 in each of the following:
(i) 2+x2+x
Solution:
The equation 2+x2+x can be written as 2+(1)x2+x
We know that, coefficient is the number which multiplies the variable.
Here, the number that multiplies the variable x2 is 1
, the coefficients of x2 in 2+x2+x is 1.
(ii) 2–x2+x3
Solution:
The equation 2–x2+x3 can be written as 2+(–1)x2+x3
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x2 is -1
the coefficients of x2 in 2–x2+x3 is -1.
(iii) (π/2)x2+x
Solution:
The equation (π/2)x2 +x can be written as (π/2)x2 + x
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x2 is π/2.
the coefficients of x2 in (π/2)x2 +x is π/2.
(iii)√2x-1
Solution:
The equation √2x-1 can be written as 0x2+√2x-1 [Since 0x2 is 0]
We know that, coefficient is the number (along with its sign, i.e., – or +) which multiplies the variable.
Here, the number that multiplies the variable x2is 0
, the coefficients of x2 in √2x-1 is 0.
3. Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
Binomial of degree 35: A polynomial having two terms and the highest degree 35 is called a binomial of degree 35
Eg., 3x35+5
Monomial of degree 100: A polynomial having one term and the highest degree 100 is called a monomial of degree 100
Eg., 4x100
4. Write the degree of each of the following polynomials:
(i) 5x3+4x2+7x
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 5x3+4x2+7x = 5x3+4x2+7x1
The powers of the variable x are: 3, 2, 1
the degree of 5x3+4x2+7x is 3 as 3 is the highest power of x in the equation.
(ii) 4–y2
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 4–y2,
The power of the variable y is 2
the degree of 4–y2 is 2 as 2 is the highest power of y in the equation.
(iii) 5t–√7
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, in 5t–√7 ,
The power of the variable t is: 1
the degree of 5t–√7 is 1 as 1 is the highest power of y in the equation.
(iv) 3
Solution:
The highest power of the variable in a polynomial is the degree of the polynomial.
Here, 3 = 3×1 = 3× x0
The power of the variable here is: 0
the degree of 3 is 0.
5. Classify the following as linear, quadratic and cubic polynomials:
Solution:
We know that,
Linear polynomial: A polynomial of degree one is called a linear polynomial.
Quadratic polynomial: A polynomial of degree two is called a quadratic polynomial.
Cubic polynomial: A polynomial of degree three is called a cubic polynomial.
(i) x2+x
Solution:
The highest power of x2+x is 2
the degree is 2
Hence, x2+x is a quadratic polynomial
(ii) x–x3
Solution:
The highest power of x–x3 is 3
the degree is 3
Hence, x–x3 is a cubic polynomial
(iii) y+y2+4
Solution:
The highest power of y+y2+4 is 2
the degree is 2
Hence, y+y2+4is a quadratic polynomial
(iv) 1+x
Solution:
The highest power of 1+x is 1
the degree is 1
Hence, 1+x is a linear polynomial.
(v) 3t
Solution:
The highest power of 3t is 1
the degree is 1
Hence, 3t is a linear polynomial.
(vi) r2
Solution:
The highest power of r2 is 2
the degree is 2
Hence, r2is a quadratic polynomial.
(vii) 7x3
Solution:
The highest power of 7x3 is 3
the degree is 3
Hence, 7x3 is a cubic polynomial.
Exercise 2.2 Page: 34
1. Find the value of the polynomial (x)=5x−4x2+3
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
Let f(x) = 5x−4x2+3
(i) When x = 0
f(0) = 5(0)-4(0)2+3
= 3
(ii) When x = -1
f(x) = 5x−4x2+3
f(−1) = 5(−1)−4(−1)2+3
= −5–4+3
= −6
(iii) When x = 2
f(x) = 5x−4x2+3
f(2) = 5(2)−4(2)2+3
= 10–16+3
= −3
2. Find p(0), p(1) and p(2) for each of the following polynomials:
(i) p(y)=y2−y+1
Solution:
p(y) = y2–y+1
∴p(0) = (0)2−(0)+1=1
p(1) = (1)2–(1)+1=1
p(2) = (2)2–(2)+1=3
(ii) p(t)=2+t+2t2−t3
Solution:
p(t) = 2+t+2t2−t3
∴p(0) = 2+0+2(0)2–(0)3=2
p(1) = 2+1+2(1)2–(1)3=2+1+2–1=4
p(2) = 2+2+2(2)2–(2)3=2+2+8–8=4
(iii) p(x)=x3
Solution:
p(x) = x3
∴p(0) = (0)3 = 0
p(1) = (1)3 = 1
p(2) = (2)3 = 8
(iv) P(x) = (x−1)(x+1)
Solution:
p(x) = (x–1)(x+1)
∴p(0) = (0–1)(0+1) = (−1)(1) = –1
p(1) = (1–1)(1+1) = 0(2) = 0
p(2) = (2–1)(2+1) = 1(3) = 3
3. Verify whether the following are zeroes of the polynomial, indicated against them.
(i) p(x)=3x+1, x=−1/3
Solution:
For, x = -1/3, p(x) = 3x+1
∴p(−1/3) = 3(-1/3)+1 = −1+1 = 0
∴ -1/3 is a zero of p(x).
(ii) p(x)=5x–π, x = 4/5
Solution:
For, x = 4/5, p(x) = 5x–π
∴ p(4/5) = 5(4/5)- π= 4-π
∴ 4/5 is not a zero of p(x).
(iii) p(x)=x2−1, x=1, −1
Solution:
For, x = 1, −1;
p(x) = x2−1
∴p(1)=12−1=1−1 = 0
p(−1)=(-1)2−1 = 1−1 = 0
∴1, −1 are zeros of p(x).
(iv) p(x) = (x+1)(x–2), x =−1, 2
Solution:
For, x = −1,2;
p(x) = (x+1)(x–2)
∴p(−1) = (−1+1)(−1–2)
= (0)(−3) = 0
p(2) = (2+1)(2–2) = (3)(0) = 0
∴−1,2 are zeros of p(x).
(v) p(x) = x2, x = 0
Solution:
For, x = 0 p(x) = x2
p(0) = 02 = 0
∴ 0 is a zero of p(x).
(vi) p(x) = lx+m, x = −m/l
Solution:
For, x = -m/l ; p(x) = lx+m
∴ p(-m/l)= l(-m/l)+m = −m+m = 0
∴-m/l is a zero of p(x).
(vii) p(x) = 3x2−1, x = -1/√3 , 2/√3
Solution:
For, x = -1/√3 , 2/√3 ; p(x) = 3x2−1
∴p(-1/√3) = 3(-1/√3)2-1 = 3(1/3)-1 = 1-1 = 0
∴p(2/√3 ) = 3(2/√3)2-1 = 3(4/3)-1 = 4−1=3 ≠ 0
∴-1/√3 is a zero of p(x) but 2/√3 is not a zero of p(x).
(viii) p(x) =2x+1, x = 1/2
Solution:
For, x = 1/2 p(x) = 2x+1
∴ p(1/2)=2(1/2)+1 = 1+1 = 2≠0
∴1/2 is not a zero of p(x).
4. Find the zero of the polynomials in each of the following cases:
(i) p(x) = x+5
Solution:
p(x) = x+5
⇒ x+5 = 0
⇒ x = −5
∴ -5 is a zero polynomial of the polynomial p(x).
(ii) p(x) = x–5
Solution:
p(x) = x−5
⇒ x−5 = 0
⇒ x = 5
∴ 5 is a zero polynomial of the polynomial p(x).
(iii) p(x) = 2x+5
Solution:
p(x) = 2x+5
⇒ 2x+5 = 0
⇒ 2x = −5
⇒ x = -5/2
∴x = -5/2 is a zero polynomial of the polynomial p(x).
(iv) p(x) = 3x–2
Solution:
p(x) = 3x–2
⇒ 3x−2 = 0
⇒ 3x = 2
⇒x = 2/3
∴x = 2/3 is a zero polynomial of the polynomial p(x).
(v) p(x) = 3x
Solution:
p(x) = 3x
⇒ 3x = 0
⇒ x = 0
∴0 is a zero polynomial of the polynomial p(x).
(vi) p(x) = ax, a≠0
Solution:
p(x) = ax
⇒ ax = 0
⇒ x = 0
∴x = 0 is a zero polynomial of the polynomial p(x).
(vii)p(x) = cx+d, c ≠ 0, c, d are real numbers.
Solution:
p(x) = cx + d
⇒ cx+d =0
⇒ x = -d/c
∴ x = -d/c is a zero polynomial of the polynomial p(x).
Exercise 2.3 Page: 40
1. Find the remainder when x3+3x2+3x+1 is divided by
(i) x+1
Solution:
x+1= 0
⇒x = −1
∴Remainder:
p(−1) = (−1)3+3(−1)2+3(−1)+1
= −1+3−3+1
= 0
(ii) x−1/2
Solution:
x-1/2 = 0
⇒ x = 1/2
∴Remainder:
p(1/2) = (1/2)3+3(1/2)2+3(1/2)+1
= (1/8)+(3/4)+(3/2)+1
= 27/8
(iii) x
Solution:
x = 0
∴Remainder:
p(0) = (0)3+3(0)2+3(0)+1
= 1
(iv) x+π
Solution:
x+π = 0
⇒ x = −π
∴Remainder:
p(0) = (−π)3 +3(−π)2+3(−π)+1
= −π3+3π2−3π+1
(v) 5+2x
Solution:
5+2x=0
⇒ 2x = −5
⇒ x = -5/2
∴Remainder:
(-5/2)3+3(-5/2)2+3(-5/2)+1 = (-125/8)+(75/4)-(15/2)+1
= -27/8
2. Find the remainder when x3−ax2+6x−a is divided by x-a.
Solution:
Let p(x) = x3−ax2+6x−a
x−a = 0
∴x = a
Remainder:
p(a) = (a)3−a(a2)+6(a)−a
= a3−a3+6a−a = 5a
3. Check whether 7+3x is a factor of 3x3+7x.
Solution:
7+3x = 0
⇒ 3x = −7
⇒ x = -7/3
∴Remainder:
3(-7/3)3+7(-7/3) = -(343/9)+(-49/3)
= (-343-(49)3)/9
= (-343-147)/9
= -490/9 ≠ 0
∴7+3x is not a factor of 3x3+7x
Exercise 2.4 Page: 43
1. Determine which of the following polynomials has (x + 1) a factor:
(i) x3+x2+x+1
Solution:
Let p(x) = x3+x2+x+1
The zero of x+1 is -1. [x+1 = 0 means x = -1]
p(−1) = (−1)3+(−1)2+(−1)+1
= −1+1−1+1
= 0
∴By factor theorem, x+1 is a factor of x3+x2+x+1
(ii) x4+x3+x2+x+1
Solution:
Let p(x)= x4+x3+x2+x+1
The zero of x+1 is -1. . [x+1= 0 means x = -1]
p(−1) = (−1)4+(−1)3+(−1)2+(−1)+1
= 1−1+1−1+1
= 1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4 + x3 + x2 + x + 1
(iii) x4+3x3+3x2+x+1
Solution:
Let p(x)= x4+3x3+3x2+x+1
The zero of x+1 is -1.
p(−1)=(−1)4+3(−1)3+3(−1)2+(−1)+1
=1−3+3−1+1
=1 ≠ 0
∴By factor theorem, x+1 is not a factor of x4+3x3+3x2+x+1
(iv) x3 – x2– (2+√2)x +√2
Solution:
Let p(x) = x3–x2–(2+√2)x +√2
The zero of x+1 is -1.
p(−1) = (-1)3–(-1)2–(2+√2)(-1) + √2 = −1−1+2+√2+√2
= 2√2 ≠ 0
∴By factor theorem, x+1 is not a factor of x3–x2–(2+√2)x +√2
2. Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x3+x2–2x–1, g(x) = x+1
Solution:
p(x) = 2x3+x2–2x–1, g(x) = x+1
g(x) = 0
⇒ x+1 = 0
⇒ x = −1
∴Zero of g(x) is -1.
Now,
p(−1) = 2(−1)3+(−1)2–2(−1)–1
= −2+1+2−1
= 0
∴By factor theorem, g(x) is a factor of p(x).
(ii) p(x)=x3+3x2+3x+1, g(x) = x+2
Solution:
p(x) = x3+3x2+3x+1, g(x) = x+2
g(x) = 0
⇒ x+2 = 0
⇒ x = −2
∴ Zero of g(x) is -2.
Now,
p(−2) = (−2)3+3(−2)2+3(−2)+1
= −8+12−6+1
= −1 ≠ 0
∴By factor theorem, g(x) is not a factor of p(x).
(iii) p(x)=x3–4x2+x+6, g(x) = x–3
Solution:
p(x) = x3–4x2+x+6, g(x) = x -3
g(x) = 0
⇒ x−3 = 0
⇒ x = 3
∴ Zero of g(x) is 3.
Now,
p(3) = (3)3−4(3)2+(3)+6
= 27−36+3+6
= 0
∴By factor theorem, g(x) is a factor of p(x).
3. Find the value of k, if x–1 is a factor of p(x) in each of the following cases:
(i) p(x) = x2+x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ (1)2+(1)+k = 0
⇒ 1+1+k = 0
⇒ 2+k = 0
⇒ k = −2
(ii) p(x) = 2x2+kx+√2
Solution:
If x-1 is a factor of p(x), then p(1)=0
⇒ 2(1)2+k(1)+√2 = 0
⇒ 2+k+√2 = 0
⇒ k = −(2+√2)
(iii) p(x) = kx2–√2x+1
Solution:
If x-1 is a factor of p(x), then p(1)=0
By Factor Theorem
⇒ k(1)2-√2(1)+1=0
⇒ k = √2-1
(iv) p(x)=kx2–3x+k
Solution:
If x-1 is a factor of p(x), then p(1) = 0
By Factor Theorem
⇒ k(1)2–3(1)+k = 0
⇒ k−3+k = 0
⇒ 2k−3 = 0
⇒ k= 3/2
4. Factorize:
(i) 12x2–7x+1
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -7 and product =1×12 = 12
We get -3 and -4 as the numbers [-3+-4=-7 and -3×-4 = 12]
12x2–7x+1= 12x2-4x-3x+1
= 4x(3x-1)-1(3x-1)
= (4x-1)(3x-1)
(ii) 2x2+7x+3
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 7 and product = 2×3 = 6
We get 6 and 1 as the numbers [6+1 = 7 and 6×1 = 6]
2x2+7x+3 = 2x2+6x+1x+3
= 2x (x+3)+1(x+3)
= (2x+1)(x+3)
(iii) 6x2+5x-6
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = 5 and product = 6×-6 = -36
We get -4 and 9 as the numbers [-4+9 = 5 and -4×9 = -36]
6x2+5x-6 = 6x2+9x–4x–6
= 3x(2x+3)–2(2x+3)
= (2x+3)(3x–2)
(iv) 3x2–x–4
Solution:
Using the splitting the middle term method,
We have to find a number whose sum = -1 and product = 3×-4 = -12
We get -4 and 3 as the numbers [-4+3 = -1 and -4×3 = -12]
3x2–x–4 = 3x2–4x+3x–4
= x(3x–4)+1(3x–4)
= (3x–4)(x+1)
5. Factorize:
(i) x3–2x2–x+2
Solution:
Let p(x) = x3–2x2–x+2
Factors of 2 are ±1 and ± 2
Now,
p(x) = x3–2x2–x+2
p(−1) = (−1)3–2(−1)2–(−1)+2
= −1−2+1+2
= 0
Therefore, (x+1) is the factor of p(x)
Now, Dividend = Divisor × Quotient + Remainder
(x+1)(x2–3x+2) = (x+1)(x2–x–2x+2)
= (x+1)(x(x−1)−2(x−1))
= (x+1)(x−1)(x-2)
(ii) x3–3x2–9x–5
Solution:
Let p(x) = x3–3x2–9x–5
Factors of 5 are ±1 and ±5
By trial method, we find that
p(5) = 0
So, (x-5) is factor of p(x)
Now,
p(x) = x3–3x2–9x–5
p(5) = (5)3–3(5)2–9(5)–5
= 125−75−45−5
= 0
Therefore, (x-5) is the factor of p(x)
Now, Dividend = Divisor × Quotient + Remainder
(x−5)(x2+2x+1) = (x−5)(x2+x+x+1)
= (x−5)(x(x+1)+1(x+1))
= (x−5)(x+1)(x+1)
(iii) x3+13x2+32x+20
Solution:
Let p(x) = x3+13x2+32x+20
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
p(-1) = 0
So, (x+1) is factor of p(x)
Now,
p(x)= x3+13x2+32x+20
p(-1) = (−1)3+13(−1)2+32(−1)+20
= −1+13−32+20
= 0
Therefore, (x+1) is the factor of p(x)
Now, Dividend = Divisor × Quotient +Remainder
(x+1)(x2+12x+20) = (x+1)(x2+2x+10x+20)
= (x+1)x(x+2)+10(x+2)
= (x+1)(x+2)(x+10)
(iv) 2y3+y2–2y–1
Solution:
Let p(y) = 2y3+y2–2y–1
Factors = 2×(−1)= -2 are ±1 and ±2
By trial method, we find that
p(1) = 0
So, (y-1) is factor of p(y)
Now,
p(y) = 2y3+y2–2y–1
p(1) = 2(1)3+(1)2–2(1)–1
= 2+1−2
= 0
Therefore, (y-1) is the factor of p(y)

Now, Dividend = Divisor × Quotient + Remainder
(y−1)(2y2+3y+1) = (y−1)(2y2+2y+y+1)
= (y−1)(2y(y+1)+1(y+1))
= (y−1)(2y+1)(y+1)
Exercise 2.5 Page: 48
1. Use suitable identities to find the following products:
(i) (x+4)(x +10)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, a = 4 and b = 10]
We get,
(x+4)(x+10) = x2+(4+10)x+(4×10)
= x2+14x+40
(ii) (x+8)(x –10)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, a = 8 and b = −10]
We get,
(x+8)(x−10) = x2+(8+(−10))x+(8×(−10))
= x2+(8−10)x–80
= x2−2x−80
(iii) (3x+4)(3x–5)
Solution:
Using the identity, (x+a)(x+b) = x 2+(a+b)x+ab
[Here, x = 3x, a = 4 and b = −5]
We get,
(3x+4)(3x−5) = (3x)2+[4+(−5)]3x+4×(−5)
= 9x2+3x(4–5)–20
= 9x2–3x–20
(iv) (y2+3/2)(y2-3/2)
Solution:
Using the identity, (x+y)(x–y) = x2–y 2
[Here, x = y2and y = 3/2]
We get,
(y2+3/2)(y2–3/2) = (y2)2–(3/2)2
= y4–9/4
2. Evaluate the following products without multiplying directly:
(i) 103×107
Solution:
103×107= (100+3)×(100+7)
Using identity, [(x+a)(x+b) = x2+(a+b)x+ab
Here, x = 100
a = 3
b = 7
We get, 103×107 = (100+3)×(100+7)
= (100)2+(3+7)100+(3×7)
= 10000+1000+21
= 11021
(ii) 95×96
Solution:
95×96 = (100-5)×(100-4)
Using identity, [(x-a)(x-b) = x2-(a+b)x+ab
Here, x = 100
a = -5
b = -4
We get, 95×96 = (100-5)×(100-4)
= (100)2+100(-5+(-4))+(-5×-4)
= 10000-900+20
= 9120
(iii) 104×96
Solution:
104×96 = (100+4)×(100–4)
Using identity, [(a+b)(a-b)= a2-b2]
Here, a = 100
b = 4
We get, 104×96 = (100+4)×(100–4)
= (100)2–(4)2
= 10000–16
= 9984
3. Factorize the following using appropriate identities:
(i) 9x2+6xy+y2
Solution:
9x2+6xy+y2 = (3x)2+(2×3x×y)+y2
Using identity, x2+2xy+y2 = (x+y)2
Here, x = 3x
y = y
9x2+6xy+y2 = (3x)2+(2×3x×y)+y2
= (3x+y)2
= (3x+y)(3x+y)
(ii) 4y2−4y+1
Solution:
4y2−4y+1 = (2y)2–(2×2y×1)+1
Using identity, x2 – 2xy + y2 = (x – y)2
Here, x = 2y
y = 1
4y2−4y+1 = (2y)2–(2×2y×1)+12
= (2y–1)2
= (2y–1)(2y–1)
(iii) x2–y2/100
Solution:
x2–y2/100 = x2–(y/10)2
Using identity, x2-y2 = (x-y)(x+y)
Here, x = x
y = y/10
x2–y2/100 = x2–(y/10)2
= (x–y/10)(x+y/10)
4. Expand each of the following, using suitable identities:
(i) (x+2y+4z)2
(ii) (2x−y+z)2
(iii) (−2x+3y+2z)2
(iv) (3a –7b–c)2
(v) (–2x+5y–3z)2
(vi)((1/4)a-(1/2)b +1)2
Solution:
(i) (x+2y+4z)2
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = x
y = 2y
z = 4z
(x+2y+4z)2 = x2+(2y)2+(4z)2+(2×x×2y)+(2×2y×4z)+(2×4z×x)
= x2+4y2+16z2+4xy+16yz+8xz
(ii) (2x−y+z)2
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 2x
y = −y
z = z
(2x−y+z)2 = (2x)2+(−y)2+z2+(2×2x×−y)+(2×−y×z)+(2×z×2x)
= 4x2+y2+z2–4xy–2yz+4xz
(iii) (−2x+3y+2z)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = −2x
y = 3y
z = 2z
(−2x+3y+2z)2 = (−2x)2+(3y)2+(2z)2+(2×−2x×3y)+(2×3y×2z)+(2×2z×−2x)
= 4x2+9y2+4z2–12xy+12yz–8xz
(iv) (3a –7b–c)2
Solution:
Using identity (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = 3a
y = – 7b
z = – c
(3a –7b– c)2 = (3a)2+(– 7b)2+(– c)2+(2×3a ×– 7b)+(2×– 7b ×– c)+(2×– c ×3a)
= 9a2 + 49b2 + c2– 42ab+14bc–6ca
(v) (–2x+5y–3z)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = –2x
y = 5y
z = – 3z
(–2x+5y–3z)2 = (–2x)2+(5y)2+(–3z)2+(2×–2x × 5y)+(2× 5y×– 3z)+(2×–3z ×–2x)
= 4x2+25y2 +9z2– 20xy–30yz+12zx
(vi) ((1/4)a-(1/2)b+1)2
Solution:
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
Here, x = (1/4)a
y = (-1/2)b
z = 1
5. Factorize:
(i) 4x2+9y2+16z2+12xy–24yz–16xz
(ii ) 2x2+y2+8z2–2√2xy+4√2yz–8xz
Solution:
(i) 4x2+9y2+16z2+12xy–24yz–16xz
Using identity, (x+y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
4x2+9y2+16z2+12xy–24yz–16xz = (2x)2+(3y)2+(−4z)2+(2×2x×3y)+(2×3y×−4z)+(2×−4z×2x)
= (2x+3y–4z)2
= (2x+3y–4z)(2x+3y–4z)
(ii) 2x2+y2+8z2–2√2xy+4√2yz–8xz
Using identity, (x +y+z)2 = x2+y2+z2+2xy+2yz+2zx
We can say that, x2+y2+z2+2xy+2yz+2zx = (x+y+z)2
2x2+y2+8z2–2√2xy+4√2yz–8xz
= (-√2x)2+(y)2+(2√2z)2+(2×-√2x×y)+(2×y×2√2z)+(2×2√2×−√2x)
= (−√2x+y+2√2z)2
= (−√2x+y+2√2z)(−√2x+y+2√2z)
6. Write the following cubes in expanded form:
(i) (2x+1)3
(ii) (2a−3b)3
(iii) ((3/2)x+1)3
(iv) (x−(2/3)y)3
Solution:
(i) (2x+1)3
Using identity,(x+y)3 = x3+y3+3xy(x+y)
(2x+1)3= (2x)3+13+(3×2x×1)(2x+1)
= 8x3+1+6x(2x+1)
= 8x3+12x2+6x+1
(ii) (2a−3b)3
Using identity,(x–y)3 = x3–y3–3xy(x–y)
(2a−3b)3 = (2a)3−(3b)3–(3×2a×3b)(2a–3b)
= 8a3–27b3–18ab(2a–3b)
= 8a3–27b3–36a2b+54ab2
(iii) ((3/2)x+1)3
Using identity,(x+y)3 = x3+y3+3xy(x+y)
((3/2)x+1)3=((3/2)x)3+13+(3×(3/2)x×1)((3/2)x +1)
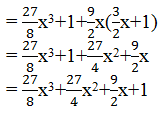
(iv) (x−(2/3)y)3
Using identity, (x –y)3 = x3–y3–3xy(x–y)
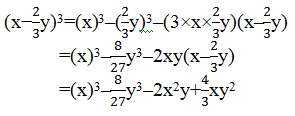
7. Evaluate the following using suitable identities:
(i) (99)3
(ii) (102)3
(iii) (998)3
Solutions:
(i) (99)3
Solution:
We can write 99 as 100–1
Using identity, (x –y)3 = x3–y3–3xy(x–y)
(99)3 = (100–1)3
= (100)3–13–(3×100×1)(100–1)
= 1000000 –1–300(100 – 1)
= 1000000–1–30000+300
= 970299
(ii) (102)3
Solution:
We can write 102 as 100+2
Using identity,(x+y)3 = x3+y3+3xy(x+y)
(100+2)3 =(100)3+23+(3×100×2)(100+2)
= 1000000 + 8 + 600(100 + 2)
= 1000000 + 8 + 60000 + 1200
= 1061208
(iii) (998)3
Solution:
We can write 99 as 1000–2
Using identity,(x–y)3 = x3–y3–3xy(x–y)
(998)3 =(1000–2)3
=(1000)3–23–(3×1000×2)(1000–2)
= 1000000000–8–6000(1000– 2)
= 1000000000–8- 6000000+12000
= 994011992
8. Factorise each of the following:
(i) 8a3+b3+12a2b+6ab2
(ii) 8a3–b3–12a2b+6ab2
(iii) 27–125a3–135a +225a2
(iv) 64a3–27b3–144a2b+108ab2
(v) 27p3–(1/216)−(9/2) p2+(1/4)p
Solutions:
(i) 8a3+b3+12a2b+6ab2
Solution:
The expression, 8a3+b3+12a2b+6ab2 can be written as (2a)3+b3+3(2a)2b+3(2a)(b)2
8a3+b3+12a2b+6ab2 = (2a)3+b3+3(2a)2b+3(2a)(b)2
= (2a+b)3
= (2a+b)(2a+b)(2a+b)
Here, the identity, (x +y)3 = x3+y3+3xy(x+y) is used.
(ii) 8a3–b3–12a2b+6ab2
Solution:
The expression, 8a3–b3−12a2b+6ab2 can be written as (2a)3–b3–3(2a)2b+3(2a)(b)2
8a3–b3−12a2b+6ab2 = (2a)3–b3–3(2a)2b+3(2a)(b)2
= (2a–b)3
= (2a–b)(2a–b)(2a–b)
Here, the identity,(x–y)3 = x3–y3–3xy(x–y) is used.
(iii) 27–125a3–135a+225a2
Solution:
The expression, 27–125a3–135a +225a2 can be written as 33–(5a)3–3(3)2(5a)+3(3)(5a)2
27–125a3–135a+225a2 =
33–(5a)3–3(3)2(5a)+3(3)(5a)2
= (3–5a)3
= (3–5a)(3–5a)(3–5a)
Here, the identity, (x–y)3 = x3–y3-3xy(x–y) is used.
(iv) 64a3–27b3–144a2b+108ab2
Solution:
The expression, 64a3–27b3–144a2b+108ab2can be written as (4a)3–(3b)3–3(4a)2(3b)+3(4a)(3b)2
64a3–27b3–144a2b+108ab2=
(4a)3–(3b)3–3(4a)2(3b)+3(4a)(3b)2
=(4a–3b)3
=(4a–3b)(4a–3b)(4a–3b)
Here, the identity, (x – y)3 = x3 – y3 – 3xy(x – y) is used.
(v) 7p3– (1/216)−(9/2) p2+(1/4)p
Solution:
The expression, 27p3–(1/216)−(9/2) p2+(1/4)p
can be written as (3p)3–(1/6)3–3(3p)2(1/6)+3(3p)(1/6)2
27p3–(1/216)−(9/2) p2+(1/4)p =
(3p)3–(1/6)3–3(3p)2(1/6)+3(3p)(1/6)2
= (3p–16)3
= (3p–16)(3p–16)(3p–16)
9. Verify:
(i) x3+y3 = (x+y)(x2–xy+y2)
(ii) x3–y3 = (x–y)(x2+xy+y2)
Solutions:
(i) x3+y3 = (x+y)(x2–xy+y2)
We know that, (x+y)3 = x3+y3+3xy(x+y)
⇒ x3+y3 = (x+y)3–3xy(x+y)
⇒ x3+y3 = (x+y)[(x+y)2–3xy]
Taking (x+y) common ⇒ x3+y3 = (x+y)[(x2+y2+2xy)–3xy]
⇒ x3+y3 = (x+y)(x2+y2–xy)
(ii) x3–y3 = (x–y)(x2+xy+y2)
We know that,(x–y)3 = x3–y3–3xy(x–y)
⇒ x3−y3 = (x–y)3+3xy(x–y)
⇒ x3−y3 = (x–y)[(x–y)2+3xy]
Taking (x+y) common ⇒ x3−y3 = (x–y)[(x2+y2–2xy)+3xy]
⇒ x3+y3 = (x–y)(x2+y2+xy)
10. Factorize each of the following:
(i) 27y3+125z3
(ii) 64m3–343n3
Solutions:
(i) 27y3+125z3
The expression, 27y3+125z3 can be written as (3y)3+(5z)3
27y3+125z3 = (3y)3+(5z)3
We know that, x3+y3 = (x+y)(x2–xy+y2)
27y3+125z3 = (3y)3+(5z)3
= (3y+5z)[(3y)2–(3y)(5z)+(5z)2]
= (3y+5z)(9y2–15yz+25z2)
(ii) 64m3–343n3
The expression, 64m3–343n3can be written as (4m)3–(7n)3
64m3–343n3 =
(4m)3–(7n)3
We know that, x3–y3 = (x–y)(x2+xy+y2)
64m3–343n3 = (4m)3–(7n)3
= (4m-7n)[(4m)2+(4m)(7n)+(7n)2]
= (4m-7n)(16m2+28mn+49n2)
11. Factorise: 27x3+y3+z3–9xyz
Solution:
The expression27x3+y3+z3–9xyz can be written as (3x)3+y3+z3–3(3x)(y)(z)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
We know that, x3+y3+z3–3xyz = (x+y+z)(x2+y2+z2–xy –yz–zx)
27x3+y3+z3–9xyz = (3x)3+y3+z3–3(3x)(y)(z)
= (3x+y+z)[(3x)2+y2+z2–3xy–yz–3xz]
= (3x+y+z)(9x2+y2+z2–3xy–yz–3xz)
12. Verify that:
x3+y3+z3–3xyz = (1/2) (x+y+z)[(x–y)2+(y–z)2+(z–x)2]
Solution:
We know that,
x3+y3+z3−3xyz = (x+y+z)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = (1/2)(x+y+z)[2(x2+y2+z2–xy–yz–xz)]
= (1/2)(x+y+z)(2x2+2y2+2z2–2xy–2yz–2xz)
= (1/2)(x+y+z)[(x2+y2−2xy)+(y2+z2–2yz)+(x2+z2–2xz)]
= (1/2)(x+y+z)[(x–y)2+(y–z)2+(z–x)2]
13. If x+y+z = 0, show that x3+y3+z3 = 3xyz.
Solution:
We know that,
x3+y3+z3-3xyz = (x +y+z)(x2+y2+z2–xy–yz–xz)
Now, according to the question, let (x+y+z) = 0,
then, x3+y3+z3 -3xyz = (0)(x2+y2+z2–xy–yz–xz)
⇒ x3+y3+z3–3xyz = 0
⇒ x3+y3+z3 = 3xyz
Hence Proved
14. Without actually calculating the cubes, find the value of each of the following:
(i) (−12)3+(7)3+(5)3
(ii) (28)3+(−15)3+(−13)3
Solution:
(i) (−12)3+(7)3+(5)3
Let a = −12
b = 7
c = 5
We know that if x+y+z = 0, then x3+y3+z3=3xyz.
Here, −12+7+5=0
(−12)3+(7)3+(5)3 = 3xyz
= 3×-12×7×5
= -1260
(ii) (28)3+(−15)3+(−13)3
Solution:
(28)3+(−15)3+(−13)3
Let a = 28
b = −15
c = −13
We know that if x+y+z = 0, then x3+y3+z3 = 3xyz.
Here, x+y+z = 28–15–13 = 0
(28)3+(−15)3+(−13)3 = 3xyz
= 0+3(28)(−15)(−13)
= 16380
15. Give possible expressions for the length and breadth of each of the following rectangles, in which their areas are given:
(i) Area : 25a2–35a+12
(ii) Area : 35y2+13y–12
Solution:
(i) Area : 25a2–35a+12
Using the splitting the middle term method,
We have to find a number whose sum = -35 and product =25×12=300
We get -15 and -20 as the numbers [-15+-20=-35 and -15×-20=300]
25a2–35a+12 = 25a2–15a−20a+12
= 5a(5a–3)–4(5a–3)
= (5a–4)(5a–3)
Possible expression for length = 5a–4
Possible expression for breadth = 5a –3
(ii) Area : 35y2+13y–12
Using the splitting the middle term method,
We have to find a number whose sum = 13 and product = 35×-12 = 420
We get -15 and 28 as the numbers [-15+28 = 13 and -15×28=420]
35y2+13y–12 = 35y2–15y+28y–12
= 5y(7y–3)+4(7y–3)
= (5y+4)(7y–3)
Possible expression for length = (5y+4)
Possible expression for breadth = (7y–3)
16. What are the possible expressions for the dimensions of the cuboids whose volumes are given below?
(i) Volume : 3x2–12x
(ii) Volume : 12ky2+8ky–20k
Solution:
(i) Volume : 3x2–12x
3x2–12x can be written as 3x(x–4) by taking 3x out of both the terms.
Possible expression for length = 3
Possible expression for breadth = x
Possible expression for height = (x–4)
(ii) Volume:
12ky2+8ky–20k
12ky2+8ky–20k can be written as 4k(3y2+2y–5) by taking 4k out of both the terms.
12ky2+8ky–20k = 4k(3y2+2y–5)
[Here, 3y2+2y–5 can be written as 3y2+5y–3y–5 using splitting the middle term method.]
= 4k(3y2+5y–3y–5)
= 4k[y(3y+5)–1(3y+5)]
= 4k(3y+5)(y–1)
Possible expression for length = 4k
Possible expression for breadth = (3y +5)
Possible expression for height = (y -1)







Hello,
May I help you ?