AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects ∠A.

Solution:

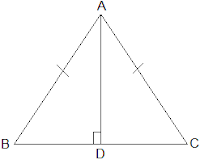
It is given that AD is an altitude and AB = AC. The diagram is as follows:

(i) In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°

AB = AC (It is given in the question)

AD = AD (Common arm)

∴ ΔABD ≅ ΔACD by RHS congruence condition.

Now, by the rule of CPCT,

BD = CD.

So, AD bisects BC

(ii) Again, by the rule of CPCT, ∠BAD = ∠CAD

Hence, AD bisects ∠A.