ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that

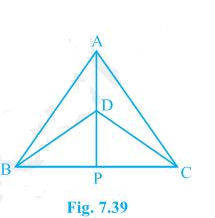
 (i) ΔABD ≅ ΔACD

(ii) ΔABP ≅ ΔACP

(iii) AP bisects ∠A as well as ∠D

(iv) AP is the perpendicular bisector of BC.

Solution:

In the above question, it is given that ΔABC and ΔDBC are two isosceles triangles.

(i) ΔABD and ΔACD are similar by SSS congruency because:

AD = AD (It is the common arm)

AB = AC (Since ΔABC is isosceles)

BD = CD (Since ΔDBC is isosceles)

∴ ΔABD ≅ ΔACD.

(ii) ΔABP and ΔACP are similar as:

AP = AP (It is the common side)

∠PAB = ∠PAC (by CPCT since ΔABD ≅ ΔACD)

AB = AC (Since ΔABC is isosceles)

So, ΔABP ≅ ΔACP by SAS congruency condition.

(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.

AP bisects ∠A. — (i)

Also, ΔBPD and ΔCPD are similar by SSS congruency as

PD = PD (It is the common side)

BD = CD (Since ΔDBC is isosceles.)

BP = CP (by CPCT as ΔABP ≅ ΔACP)

So, ΔBPD ≅ ΔCPD.

Thus, ∠BDP = ∠CDP by CPCT. — (ii)

Now by comparing (i) and (ii) it can be said that AP bisects ∠A as well as ∠D.

(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ΔCPD)

and BP = CP — (i)

also,

∠BPD +∠CPD = 180° (Since BC is a straight line.)

⇒ 2∠BPD = 180°

⇒ ∠BPD = 90° —(ii)

Now, from equations (i) and (ii), it can be said that

AP is the perpendicular bisector of BC.