Exercise 14.3 Page No: 227
1. Carry out the following divisions.
(i) 28x4 ÷ 56x
(ii) –36y3 ÷ 9y2
(iii) 66pq2r3 ÷ 11qr2
(iv) 34x3y3z3 ÷ 51xy2z3
(v) 12a8b8 ÷ (– 6a6b4)
Solution:
(i)28x4 = 2×2×7×x×x×x×x
56x = 2×2×2×7×x
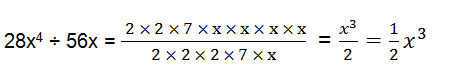
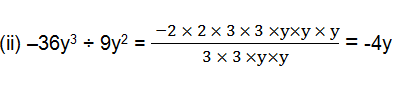
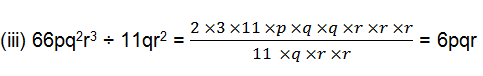
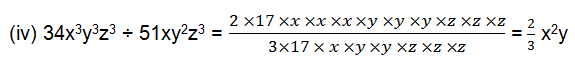
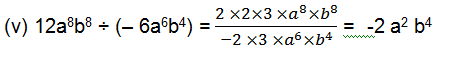
2. Divide the given polynomial by the given monomial.
(i)(5x2–6x) ÷ 3x
(ii)(3y8–4y6+5y4) ÷ y4
(iii) 8(x3y2z2+x2y3z2+x2y2z3)÷ 4x2 y2 z2
(iv)(x3+2x2+3x) ÷2x
(v) (p3q6–p6q3) ÷ p3q3
Solution:
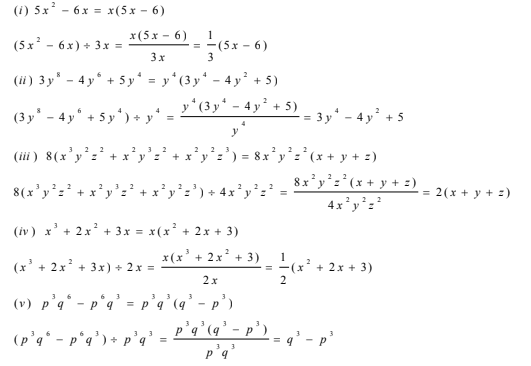
3. Work out the following divisions.
(i) (10x–25) ÷ 5
(ii) (10x–25) ÷ (2x–5)
(iii) 10y(6y+21) ÷ 5(2y+7)
(iv) 9x2y2(3z–24) ÷ 27xy(z–8)
(v) 96abc(3a–12)(5b–30) ÷ 144(a–4)(b–6)
Solution:
(i) (10x–25) ÷ 5 = 5(2x-5)/5 = 2x-5
(ii) (10x–25) ÷ (2x–5) = 5(2x-5)/( 2x-5) = 5
(iii) 10y(6y+21) ÷ 5(2y+7) = 10y×3(2y+7)/5(2y+7) = 6y
(iv) 9x2y2(3z–24) ÷ 27xy(z–8) = 9x2y2×3(z-8)/27xy(z-8) = xy
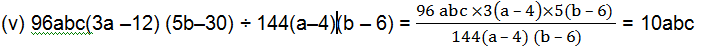
4. Divide as directed.
(i) 5(2x+1)(3x+5)÷ (2x+1)
(ii) 26xy(x+5)(y–4)÷13x(y–4)
(iii) 52pqr(p+q)(q+r)(r+p) ÷ 104pq(q+r)(r+p)
(iv) 20(y+4) (y2+5y+3) ÷ 5(y+4)
(v) x(x+1) (x+2)(x+3) ÷ x(x+1)
Solution:
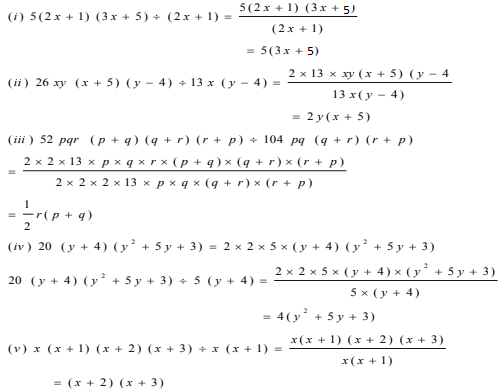
5. Factorise the expressions and divide them as directed.
(i) (y2+7y+10)÷(y+5)
(ii) (m2–14m–32)÷(m+2)
(iii) (5p2–25p+20)÷(p–1)
(iv) 4yz(z2+6z–16)÷2y(z+8)
(v) 5pq(p2–q2)÷2p(p+q)
(vi) 12xy(9x2–16y2)÷4xy(3x+4y)
(vii) 39y3(50y2–98) ÷ 26y2(5y+7)
Solution:
(i) (y2+7y+10)÷(y+5)
First solve for equation, (y2+7y+10)
(y2+7y+10) = y2+2y+5y+10 = y(y+2)+5(y+2) = (y+2)(y+5)
Now, (y2+7y+10)÷(y+5) = (y+2)(y+5)/(y+5) = y+2
(ii) (m2–14m–32)÷ (m+2)
Solve for m2–14m–32, we have
m2–14m–32 = m2+2m-16m–32 = m(m+2)–16(m+2) = (m–16)(m+2)
Now, (m2–14m–32)÷(m+2) = (m–16)(m+2)/(m+2) = m-16
(iii) (5p2–25p+20)÷(p–1)
Step 1: Take 5 common from the equation, 5p2–25p+20, we get
5p2–25p+20 = 5(p2–5p+4)
Step 2: Factorize p2–5p+4
p2–5p+4 = p2–p-4p+4 = (p–1)(p–4)
Step 3: Solve original equation
(5p2–25p+20)÷(p–1) = 5(p–1)(p–4)/(p-1) = 5(p–4)
(iv) 4yz(z2 + 6z–16)÷ 2y(z+8)
Factorize z2+6z–16,
z2+6z–16 = z2-2z+8z–16 = (z–2)(z+8)
Now, 4yz(z2+6z–16) ÷ 2y(z+8) = 4yz(z–2)(z+8)/2y(z+8) = 2z(z-2)
(v) 5pq(p2–q2) ÷ 2p(p+q)
p2–q2 can be written as (p–q)(p+q) using identity.
5pq(p2–q2) ÷ 2p(p+q) = 5pq(p–q)(p+q)/2p(p+q) = 5/2q(p–q)
(vi) 12xy(9x2–16y2) ÷ 4xy(3x+4y)
Factorize 9x2–16y2 , we have
9x2–16y2 = (3x)2–(4y)2 = (3x+4y)(3x-4y) using identity: p2–q2 = (p–q)(p+q)
Now, 12xy(9x2–16y2) ÷ 4xy(3x+4y) = 12xy(3x+4y)(3x-4y) /4xy(3x+4y) = 3(3x-4y)
(vii) 39y3(50y2–98) ÷ 26y2(5y+7)
st solve for 50y2–98, we have
50y2–98 = 2(25y2–49) = 2((5y)2–72) = 2(5y–7)(5y+7)
Now, 39y3(50y2–98) ÷ 26y2(5y+7) =
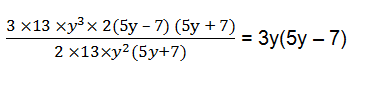



Hello,
May I help you ?