Exercise 14.1 Page No: 208
1. Find the common factors of the given terms.
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14 pq, 28p2q2
(iv) 2x, 3x2, 4
(v) 6 abc, 24ab2, 12a2b
(vi) 16 x3, – 4x2 , 32 x
(vii) 10 pq, 20qr, 30 rp
(viii) 3x2y3 , 10x3y2 , 6x2y2z
Solution:
(i) Factors of 12x and 36
12x = 2×2×3×x
36 = 2×2×3×3
Common factors of 12x and 36 are 2, 2, 3
and , 2×2×3 = 12
(ii) Factors of 2y and 22xy
2y = 2×y
22xy = 2×11×x×y
Common factors of 2y and 22xy are 2, y
and ,2×y = 2y
(iii) Factors of 14pq and 28p2q
14pq = 2x7xpxq
28p2q = 2x2x7xpxpxq
Common factors of 14 pq and 28 p2q are 2, 7 , p , q
and, 2x7xpxq = 14pq
(iv) Factors of 2x, 3x2and 4
2x = 2×x
3x2= 3×x×x
4 = 2×2
Common factors of 2x, 3x2 and 4 is 1.
(v) Factors of 6abc, 24ab2 and 12a2b
6abc = 2×3×a×b×c
24ab2 = 2×2×2×3×a×b×b
12 a2 b = 2×2×3×a×a×b
Common factors of 6 abc, 24ab2 and 12a2b are 2, 3, a, b
and, 2×3×a×b = 6ab
(vi) Factors of 16x3 , -4x2and 32x
16 x3 = 2×2×2×2×x×x×x
– 4x2 = -1×2×2×x×x
32x = 2×2×2×2×2×x
Common factors of 16 x3 , – 4x2 and 32x are 2,2, x
and, 2×2×x = 4x
(vii) Factors of 10 pq, 20qr and 30rp
10 pq = 2×5×p×q
20qr = 2×2×5×q×r
30rp= 2×3×5×r×p
Common factors of 10 pq, 20qr and 30rp are 2, 5
and, 2×5 = 10
(viii) Factors of 3x2y3 , 10x3y2 and 6x2y2z
3x2y3 = 3×x×x×y×y×y
10x3 y2 = 2×5×x×x×x×y×y
6x2y2z = 3×2×x×x×y×y×z
Common factors of 3x2y3, 10x3y2 and 6x2y2z are x2, y2
and, x2×y2 = x2y2
2.Factorise the following expressions
(i) 7x–42
(ii) 6p–12q
(iii) 7a2+ 14a
(iv) -16z+20 z3
(v) 20l2m+30alm
(vi) 5x2y-15xy2
(vii) 10a2-15b2+20c2
(viii) -4a2+4ab–4 ca
(ix) x2yz+xy2z +xyz2
(x) ax2y+bxy2+cxyz
Solution:


(vii) 10a2-15b2+20c2
10a2 = 2×5×a×a
– 15b2 = -1×3×5×b×b
20c2 = 2×2×5×c×c
Common factor of 10 a2 , 15b2 and 20c2 is 5
10a2-15b2+20c2 = 5(2a2-3b2+4c2 )
(viii) – 4a2+4ab-4ca
– 4a2 = -1×2×2×a×a
4ab = 2×2×a×b
– 4ca = -1×2×2×c×a
Common factor of – 4a2 , 4ab , – 4ca are 2, 2, a i.e. 4a
So,
– 4a2+4 ab-4 ca = 4a(-a+b-c)
(ix) x2yz+xy2z+xyz2
x2yz = x×x×y×z
xy2z = x×y×y×z
xyz2 = x×y×z×z
Common factor of x2yz , xy2z and xyz2 are x, y, z i.e. xyz
Now, x2yz+xy2z+xyz2 = xyz(x+y+z)
(x) ax2y+bxy2+cxyz
ax2y = a×x×x×y
bxy2 = b×x×y×y
cxyz = c×x×y×z
Common factors of a x2y ,bxy2 and cxyz are xy
Now, ax2y+bxy2+cxyz = xy(ax+by+cz)
3. Factorise.
(i) x2+xy+8x+8y
(ii) 15xy–6x+5y–2
(iii) ax+bx–ay–by
(iv) 15pq+15+9q+25p
(v) z–7+7xy–xyz
Solution:
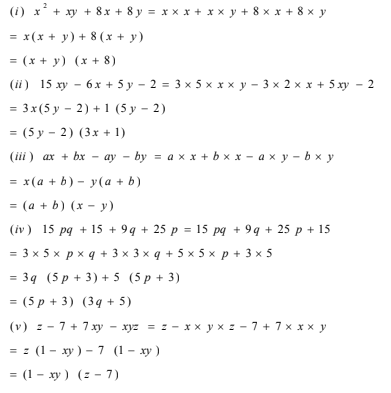



Hello,
May I help you ?